Soal - Soal tentang Relasi, Komposisi, dan Invers

Contoh Relasi
A = {1,2,3,4} dan B = {1,2,3,4,5,6} jika dikaitkan, maka hubungannya adalah A merupakan setengah dari B. Relasi tersebut dapat digambarkan dalam diagram berikut:

Fungsi Komposisi
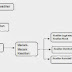
Menggabungkan dua buah fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Apa yang dilakukan tersebut dapat disebut dengan mengkomposisikan fungsi dan hasilnya disebut komposisi fungsi.

Pada diagram di atas fungsi f dikomposisikan dengan fungsi g menghasilkan fungsi h. h dinamakan fungsi komposisi dari fungsi f dan g, dinotasikan h = f o g (biasa dibaca dengan f komposisi g atau f bundaran g). Jika dirinci, maka sebagai berikut:

                 g(y) = g(f(x))

                 h(x) = g(f(x)) atau h(x) = (g o  f) (x) = g(f(x))

Contoh soal:
Jika f(x) = 2x2 + 1 dan g(x) = x + 2, tentukan:

               (g o  f) (x)

              (g o  f) (5)

               (f o g) (x)

              (f o g) (3)

Jawab:

Mengkomposisikan fungsi sebenarnya sangat sederhana, hanya perlu menaati asas ketika memasukkan nilai x.

               (g o f) (x) = g(f(x)) = g(2x2 + 1) = 2x2 + 1 + 2 = 2x2 + 3

              (g o f) (5) = 2(5)2 + 3 = 53

               (f o g) (x) = f(g(x)) = f(x + 2) = 2(x + 2)2 + 1= 2(x2 + 4x + 4) + 1 = 2x2 + 8x + 8 + 2 = 2x2 + 8x + 9

              (f o g) (x) = 2(3)2 + 8(3) + 9 = 51


Fungsi Invers
Misal ada fungsi f : A ->  B, maka invers fungsi dari f dinyatakan dengan f – 1 : B ->  A. Jika y = f(x) maka x = f-1(y). Hasil invers dari suatu fungsi dapat merupakan fungsi atau bukan fungsi. Kapan invers suatu fungsi merupakan fungsi juga? Jawabannya adalah ketika fungsi tersebut berkorespondensi satu-satu. Ketika suatu fungsi bukan merupakan korespondensi satu-satu maka inversnya bukan merupakan sebuah fungsi melainkan suatu relasi.
Contoh 1:

Tentukan invers dari fungsi f(x) = 2x + 6.

Pembahasan:

Misalnya

y = 2x + 6

2x = y – 6

x = 1/2y – 3

dengan demikian f-1(y) = 1/2y – 3 atau f-1(x) = 1/2x – 3

Contoh 2

Tentukan invers dari fungsi y = (2x + 3) / (4x + 5)

Jawab:

y = (2x + 3) / (4x + 5)

y(4x + 5) = 2x + 3

4xy + 5y = 2x + 3

4xy – 2x = 3 – 5y

x(4y – 2) = 3 – 5y

x = (3 – 5y) / (4y – 2) atau

x = ( -5y + 3) / (4y – 2)
Jadi dengan demikian f-1(y)=(2x + 3) /4x + 5=(-5y +3) / (4y – 2) atau f-1(y)=(-5x+3) / (4y – 2)

Penyelesaian contoh soal 2 fungsi komposisi bisa dikerjakan dengan menggunakan rumus cepat, yaitu jika f(x) = (ax + b) / (cx + d) maka inversnya f-1(x) = (-dx + b) / (cx – a)

NAMA    : RIZKI AMALIA
NPM    : 17513912